代入を使わずに状態を表現する
最近、SICPのWeb版が存在する事に気づいて、空いた時間にちょろちょろと読んでいた。SICPって有名だし軽く目を通しておくかな、ってくらいの気持ちだったんだけど、3章、特に3.5章のストリームの話はめちゃくちゃ面白くて興味深かったので、ブログにもまとめて置く事にした。
ストリームというのは「状態の変遷を並びとして表現するデータ構造」で、特に3.5章では遅延評価されるリストとして実装されていた。代入を使わずに状態の変遷を表現する事が出来るという意味で、大変興味深い。
状態の変遷を並びとして表現するとは?
通常、状態の変遷というのは変数への再代入によって表現される。例えば、ある変数iの状態が1から10まで変化するといった場合、
for (int i = 1; i < 11; i++) { printf("%i\n", i); }
の様に、変数iに次々と新しい値を代入する事で状態の変化を表現する。
一方、並びとして状態を表現するというのは、1から10までの値の変化を[1 2 3 4 5 6 7 8 9 10]のような1から10までの値が順に並ぶリストで表現する事に相当する。つまり、「次の状態への変化」を「並びの次の要素を返す事」として表現出来るという事である。
上記のコードと同様の事をしたければ、リストの各要素に対してprintf関数を適用すれば良くて、例えばunderscore.jsのeachメソッドの様なものを考えれば、
_.each([1, 2, 3, 4, 5, 6, 7, 8, 9, 10], function(i) { console.log(i); });
の様に各要素に対して順に関数を適用する形で表現出来る。
ここまでの例から、並びによって状態を表現する事には成功した。ただ、上記の例では最初から変遷する状態が(1から10までと)固定されていたから有限の長さのリストで表現出来たが、実際には次の状態がユーザーからの入力によって決まったり、プロセスが停止しない限りは永遠に変遷が続いたりする事もあり得る。そこで、 遅延評価 という概念が登場する事になる。
遅延評価 とは必要になるまで値の評価を送らせられるような評価方法の事で、 遅延評価 を用いればユーザーの入力が無いと表現出来ない要素を持つリストを作ったり、無限の長さを持つリストを作ったり出来る。
この 遅延評価 されるリストの事を、この場では特別なデータ構造として ストリーム と呼ぶ事にする。
ストリームの実装
SICPにおいてはscheme(LISPの方言の一つで、シンプルさがウリ)を用いて様々な概念の説明や実装がなされていたので、ここでもschemeを用いてストリームを実装したいと思う。
その前に、まずは通常のリストがschemeにおいてはどの様に表現されるかを説明する。
schemeにおけるリスト
scheme(というかLISP)においては、基本のデータ構造は値の ペア となっている。下図はSICPの図2.2から借用したもので、1と2のペアを表現している。
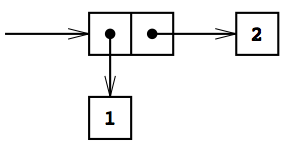
ペア はcons関数を2つの引数に適用する事で作る事が出来る。例えば、上記の1と2のペアは
(cons 1 2)
というコードを評価する事で作る事が出来る。ちなみに、schemeのコードは括弧で囲った第一要素が「関数」、それ以降に続く要素が「引数」として評価される。
この ペア を入れ子にする事で「リスト」と呼ばれるデータ構造を作る事が出来る。(ちなみに、schemeにおけるリストは、一般的なデータ構造の名称で呼ぶなら「連結リスト」である)
下図は、SICPの図2.4から借用した借用したもので、1から4までの整数からなるリストを表現している。
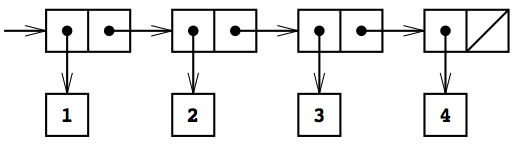
schemeのコードで表せば、
(cons 1 (cons 2 (cons 3 (cons 4 nil))))
を評価する事で上図のリストが返ってくる。また、任意の数の引数を受け取ってリストを生成出来るlist関数を使えば、
(list 1 2 3 4)
というコードでも良い。実行結果のリスト構造は、(1 2 3 4)という括弧でか囲まれた要素の並びとして表現される。
ペアやリストから要素を取り出すには、carやcdrという関数を使う。carはペアの第一要素を返す関数で、リストに適用しても第一要素が返る事になる。コードで書くと
(car (cons 1 2)) ;; 1が返る (car (list 3 4 5 6 7)) ;; 3が返る
の様な感じになる。cdrがペアの第二要素を返す関数で、リストに適用すると第二要素以降の要素からなるリストが返ってくる。
(cdr (cons 1 2)) ;; 2が返る (cdr (list 3 4 5 6 7)) ;; (4 5 6 7)が返る
これは、(list 3 4 5 6 7)が(cons 3 (list 4 5 6 7))と等価である事を考えればすんなり理解出来る。
carやcdrをくみ合わせれば、リストの任意の要素にアクセスする事が出来る。
(car (cdr (list 3 4 5 6 7))) ;; (4 5 6 7)というリストにcarを適用する事になるので、第二要素である4が返る
つまり、carやcdrがあれば、リストを操作する任意の処理を行う事が出来る。
ここまでで、リストを表現するにはcons, car, cdrが定義されれば良い事が分かった。
遅延評価されるリスト(ストリーム)を実装する
次に、遅延評価されるリストを実装する方法を考える。要は新しくそれ用のcons-stream, stream-car, stream-cdrを定義してやれば良い。
これらの内、特にのcons-streamの定義には、delayと呼ばれる関数(より正確には特殊形式)を使う。schemeにおいては、通常はコード内の各要素は評価がなされてから使われる(例えば(+ 1 (+ 1 2))のようなコードは先に内部の(+ 1 2)が3へと評価されてから(+ 1 3)の評価が行われる)んだけど、(delay <exp>)を評価する際には式<exp>は評価されず、 遅延オブジェクト と呼ばれるものが返ってくる。これは将来のある時点で<exp>を評価する「約束」と見なす事が出来て、 遅延オブジェクト に対してはforceという関数を適用した時に始めて内部の<exp>の評価が行われる。
大体のscheme処理系ではdelayやforceは組み込みで実装されている。例えばgaucheという処理系では
(delay (+ 1 2)) ;; #<promise 0x10068ee40> (force (delay (+ 1 2))) ;; 3
の様に#<promise 0x10068ee40>という形で遅延オブジェクトが表現され、forceを適用する事で内部の(+ 1 2)という式が評価される。
ぶっちゃけ上記の例だと何が嬉しいか分からないと思うけど、例えばdelayを使えばまだ存在しない変数を用いた計算式を遅延オブジェクトとして表現出来たりする。schemeではdefine関数を使って変数や関数の定義を行うんだけど、
(define x (delay (+ a b)))
の様に存在しない変数a, bを用いる遅延オブジェクトxを定義する事が出来る。変数aが未定義の状態でforceを適用すると、Errorが発生する。
(force x) ;; *** ERROR: unbound variable: a
一方、変数a, bを定義してからもう一度forceを適用すれば、ちゃんとした結果が得られる。
(define a 1) (define b 2) (force x) ;; 3が返る。
このように評価自体を送らせる事が出来るのが、遅延オブジェクトの大きな特徴である。
delayを実装する
delayは処理系で組み込みで実装されていると書いたけど、マクロとして自分で定義する事も出来る。
schemeにおけるマクロは、コードの置き換えを行う機能と考える事が出来る。例えば、(nil! x)を(setq x nil)に置換えられるべきマクロとして定義するには、
(define-syntax nil! (syntax-rules () ((_ x) (set! x '()))))
と書けば良い。(参考: https://www.shido.info/lisp/scheme_syntax.html)
define-syntaxがマクロ定義の為の関数で、第一引数としてマクロ名(上記の例ではnil!)、第二引数としてマクロの実体を受け取る。syntx-rulesがマクロを構成する為の関数で、第一引数は大抵空のリスト、第二引数に変換元と変換先の形式を記述したリストを渡す。_はマクロ名を表しているので、上記のコードは(nil! x)を(set! x '())へ変換するという意味になる。
実際、(nil! x)を実行すると確かにxにnilがsetされる。
(define x 1) ;; xには1がsetされている (nil! x) ;; xには()がsetされている
nil!と同様に、delayも(delay <exp>)を(lambda () <exp>)へと変換するマクロとして定義出来る。(lambdaは無名関数を作る関数)
(define-syntax delay (syntax-rules () ((_ exp) (lambda () exp))))
すなわち、delayがマクロとして定義された場合には、
(define x (delay (+ a b)))
というコードは
(define x (lambda () (+ a b)))
というコードへと置換えられる事になる。これは、xが引数を受け取らずに(+ a b)の実行結果を返す関数として定義される事を意味している。別の表現を用いれば、上記のコードは
(define (x) (+ a b))
と等価である。この時、遅延オブジェクトというのは単なる関数なので、forceはただの関数呼び出しとして実装出来る。
(define (force delayed-object) (delayed-object))
ここまでで、delayとforceの定義には成功した。
ちなみに、delayとforceとしてはquoteとevalを用いる形式でも上手く定義出来そう。
;; delayの定義 (define-syntax delay (syntax-rules () ((_ exp) (quote exp)))) ;; forceの定義 (define (force delayed-object) (eval delayed-object (interaction-environment)))
ちょろっと試した感じだと、問題無く動きそうだった。
遅延評価されるリスト
delayを用いてcons-streamを定義する。cons-streamは、
(cons-stream <a> <b>)
が
(cons <a> (delay <b>))
と置換えられるようなマクロとして実装すれば良い。つまり、
(define-syntax cons-stream (syntax-rules () ((_ a b) (cons a (delay b)))))
となる。consで作られたペアのうち2つ目の要素が 遅延オブジェクト になっているのがおおきな特徴で、評価はstream-cdr適用時に行われる。
;; stream-carの定義 (define (stream-car stream) (car stream)) ;; stream-cdrの定義 (define (stream-cdr stream) (force (cdr stream)))
こうして、cdr以降(第二引数以降)の評価が遅延されるリストを作れる様になった。
streamの表現力はめちゃめちゃ高くて、例えば無限に1が続くストリームであるonesは次のコードで定義出来る。
(define ones (cons-stream 1 ones))
このコードは「onesとは先頭が1でその後にones(つまり1が無限に続くリスト)が続くリスト」って事を表現してて、抽象度の高い表現をそのままコードに落とし込めている。また、無限リストを表現出来るのもそもそも遅延評価のお陰である。
整数の並びももちろん表現出来る。
;; 無限に続く整数の並びであるintegersを定義 (define integers (cons-stream 1 (add-streams ones integers))) ;; add-streamを定義 (define (add-streams s1 s2) (stream-map + s1 s2)) ;; stream-mapを定義 (define (stream-map proc . argstreams) (if (stream-null? (car argstreams)) the-empty-stream (cons-stream (apply proc (map stream-car argstreams)) (apply stream-map (cons proc (map stream-cdr argstreams)))))) ;; the-empty-streamを定義 (define the-empty-stream '()) ;; stream-null?を定義 (define (stream-null? stream) (null? stream))
上記のコードでは、二つのストリームを受け取ってそれらを要素毎に足し合わせた新しいstreamを返すadd-streamを定義してから、add-streamを用いて無限に続く整数の並びであるintegersを定義している。integersの定義の仕方も面白くて、「整数というのは1から始まっていて、その後に『『1から始まる整数の並び』の各要素に1ずつ足したもの』が続く」という抽象度の高い表現がなされている。
ones, integersともに自身の定義に自身が登場するという再帰的な構造になっているのも面白い。ストリームは数列とも見なせて、ストリーム同士の抽象度の高い関係性がコードでそのまま表現出来たりする。
引数としてストリームSをとり, その要素がS0, S0 + S1, S0 + S1 + S2, ... となるようなストリームを返す関数partial-sumsも、簡単に定義出来る。
(define (partial-sums s) (cons-stream (stream-car s) (add-streams (stream-cdr s) (partial-sums s))))
反復をストリームとして表現する
ストリームが実装できたので、最初に意図していた「ストリームでの状態の表現」を考える。
例えば何かしらの反復処理が必要になる状況を考える。SICPで例として挙げられていたのは「ニュートン法によって平方根を求める問題」で、ストリームを用いない場合には手続きの逐次的な実行(状態変数の逐次的な更新)で反復処理がなされる。
;; 平方根を求める関数sqrt-iter (define (sqrt-iter guess x) (if (good-enough? guess x) guess (sqrt-iter (improve guess x) x))) ;; guessの値の更新 (define (improve guess x) (average guess (/ x guess))) ;; 停止条件 (define (good-enough? guess x) (< (abs (- (square guess) x)) 0.001))
一方、ストリームを用いた場合には、値の変遷は並びとして表現される。
;; 更新されて行く値の並びであるstream (define (sqrt-stream x) (define guesses (cons-stream 1.0 (stream-map (lambda (guess) (improve guess x)) guesses))) guesses) ;; streamの各要素を出力 (display-stream (sqrt-stream 2)) ;; 1.0 ;; 1.5 ;; 1.4166666666666665 ;; 1.4142156862745097 ;; 1.4142135623746899 ;; 1.414213562373095 ;; ...
sqrt-streamを引数に適用した結果、例えば(sqrt-stream 2)が返すのはあくまでストリームという データ構造 であるというのがポイントで、ストリームを受け取ってストリームを返す関数等を使って様々な手続きを施す事が出来る。
ストリームを用いて微分方程式を解く
微分方程式を数値的に解く場合、通常は離散的なステップ毎に次の値の計算を繰り返す。この手続きを記述する事を考えたとき、ストリームを用いる場合にはかなり抽象度の高い表現が出来る。
例えば、「dy/dt = f(y)」を数値的に解く(yのtに対する関数形を求める)場合を考える。この問題は、次のsolve関数を用いて解く事が出来る。
;; dy/dt = f(y) を数値的に解く為の関数solveを定義。引数としては、t = 0におけるyの初期値y0, tのステップ幅dtを受け取る。返されるのは、dtで刻まれた各tにおけるyの値の並びであるストリーム。 (define (solve f y0 dt) (define y (integral (delay dy) y0 dt)) (define dy (stream-map f y)) y) ;; 非積分関数のストリーム、初期値、ステップ幅を与える事で積分された関数のストリームを返す関数ingtegraを定義。 (define (integral delayed-integrand initial-value dt) (define int (cons-stream initial-value (let ((integrand (force delayed-integrand))) (add-streams (scale-stream integrand dt) int)))))
注目して欲しいのはsolve関数の定義で、内部ではyとdyの定義を行っているだけ、しかもその定義も「yはdy/dtを積分したものでありdy/dtはfにyを適用したものである」というかなり抽象度の高い表現になっている事である。これでもきちんと計算は実行される。
この場合も、時とともに変化していく値としてでは無く時間を変数とした値の並びとしての表現がなされている。
Functional Reactive Programmingとの関連
SICPを読んでて最初に「ストリーム」という単語や「代入ではなく並びによって状態の変化を記述する」という表現を見た時に、最近流行りのFRPのストリームを思い出した。 で、気になったのでちょろっと調べたけどこのへんの関連について言及してるページとかはあんまり多く無かった。
このページで自分と同じ様な疑問を持った人がいたっぽくて、質問と返答が載ってた。
まずFRPのストリームは[(Time,[a])]みたいな型を持つみたいで、今回実装したストリームとはTimeの有無で違いがある。今回実装したストリームはストリーム内での順序の情報しかないから別のストリームとのmergeとかが出来ないけど、[(Time,[a])]型であればTimeの値によって明確にどちらが先かが定義出来るので、mergeが可能である。
後、FRPのストリームの実装には「遅延評価されるリスト」以外にも様々な実装方法があるらしく、例えばObserver Patternが使用されていたりするらしい。確かに、Bacon.jsのソースちょろっとだけ読んだ感じだと、ストリーム生成の際にはDOMオブジェクトとかに対してイベントリスナの登録とかしてるっぽかった。上手くラップして隠蔽して、外からは並びとして見えるストリームを作ってるっぽい。
別のページではSICPのstreamに触れた後により進んだ議論として FRP を紹介してたから、同じ方向性を目指してるってのはあながち間違いではないのかもしれない。そもそもSICPがかなり古くて初等的な内容を扱ってる本だから、わざわざ議論の種にならないのかもしれない。
まとめ
並びとして状態の変遷を表現する方法を確認し、その為のデータ構造としてストリームと呼ばれる遅延評価されるリスト構造を定義した。schemeにおいては、たった2つのマクロ(delayとstream-cons)を定義するだけでこれだけ豊かな表現が出来るのが驚きで、とても興味深かった。
個人的に興味を持ってる(&世間的にも注目を集めてるっぽい)FRPにも繋がりそうで、勉強になって良かった。ついでに、FRPももうちょっと調べたい。